using UnityEngine;
using System.Collections;

public class Rigid_Bunny : MonoBehaviour
{
	bool launched = false;
	float dt = 0.015f;
	[SerializeField] float gravity = 9.8f; // gravity
	[SerializeField] Vector3 v = new Vector3(0, 0, 0);  // velocity
	[SerializeField] Vector3 w = new Vector3(0, 0, 0);  // angular velocity

	[SerializeField, Range(0, 1)] float ut = 0.5f; // 摩擦系数

	float mass;                                 // mass
	Matrix4x4 I_ref;                            // reference inertia

	float linear_decay = 0.999f;                // for velocity decay
	float angular_decay = 0.98f;
	float restitution = 0.5f;                   // for collision


	// Use this for initialization
	void Start()
	{
		Mesh mesh = GetComponent<MeshFilter>().mesh;
		Vector3[] vertices = mesh.vertices;

		float m = 1;
		mass = 0;
		for (int i = 0; i < vertices.Length; i++)
		{
			mass += m;
			float diag = m * vertices[i].sqrMagnitude;
			I_ref[0, 0] += diag;
			I_ref[1, 1] += diag;
			I_ref[2, 2] += diag;
			I_ref[0, 0] -= m * vertices[i][0] * vertices[i][0];
			I_ref[0, 1] -= m * vertices[i][0] * vertices[i][1];
			I_ref[0, 2] -= m * vertices[i][0] * vertices[i][2];
			I_ref[1, 0] -= m * vertices[i][1] * vertices[i][0];
			I_ref[1, 1] -= m * vertices[i][1] * vertices[i][1];
			I_ref[1, 2] -= m * vertices[i][1] * vertices[i][2];
			I_ref[2, 0] -= m * vertices[i][2] * vertices[i][0];
			I_ref[2, 1] -= m * vertices[i][2] * vertices[i][1];
			I_ref[2, 2] -= m * vertices[i][2] * vertices[i][2];
		}
		I_ref[3, 3] = 1;
	}

	Matrix4x4 Get_Cross_Matrix(Vector3 a)
	{
		//Get the cross product matrix of vector a
		Matrix4x4 A = Matrix4x4.zero;
		A[0, 0] = 0;
		A[0, 1] = -a[2];
		A[0, 2] = a[1];
		A[1, 0] = a[2];
		A[1, 1] = 0;
		A[1, 2] = -a[0];
		A[2, 0] = -a[1];
		A[2, 1] = a[0];
		A[2, 2] = 0;
		A[3, 3] = 1;
		return A;
	}

	//In this function, update v and w by the impulse due to the collision with
	//  a plane <P, N>
	void Collision_Impulse(Vector3 P, Vector3 N)
	{
		Mesh mesh = GetComponent<MeshFilter>().mesh;
		Vector3[] vertices = mesh.vertices;
		Vector3 x = transform.position;
		Matrix4x4 R = Matrix4x4.Rotate(transform.rotation);
        
        // 统计所有产生碰撞的顶点 
		int[] vid_collision = new int[vertices.Length];
		int num_collision = 0;
		for (int i = 0; i < vertices.Length; i++)
		{
			Vector3 new_x = x + R.MultiplyPoint(vertices[i]);
			if (Vector3.Dot(new_x - P, N) < 0)
			{
				Vector3 new_v = v + Vector3.Cross(w, R.MultiplyVector(vertices[i]));
				float direction = Vector3.Dot(new_v, N);
				if (direction < 0)
				{
					vid_collision[num_collision] = i;
					num_collision++;
				}
			}
		}
		if (num_collision == 0)
		{
			return;
		}
		
        // 计算产生碰撞的平均位置和平均速度
		Vector3 ri = new Vector3(0, 0, 0);
		for (int i = 0; i < num_collision; i++)
		{
			ri += vertices[vid_collision[i]];
		}
		ri = ri / (float)(num_collision);
		Vector3 Rri = R.MultiplyVector(ri);
		Vector3 vi = v + Vector3.Cross(w, Rri);
		if (Vector3.Dot(vi, N) > 0) return;
		
        // 更新碰撞状态
		UpdateStateByCollision(N, vi, Rri);
	}

	void UpdateStateByCollision(Vector3 N, Vector3 vi, Vector3 Rri)
	{
		Vector3 v_ni = Vector3.Dot(vi, N) * N; // 计算垂直方向的速度
		Vector3 v_ti = vi - v_ni; // 计算切线方向的速度
		float a = Mathf.Max(1 - ut * (1 + restitution) * v_ni.magnitude / v_ti.magnitude, 0);
		v_ni = -restitution * v_ni; // 计算新的垂直方向速度（与弹力有关）
		v_ti = a * v_ti; // 计算新的切线方向速度（与摩擦有关）
		Vector3 new_vi = v_ni + v_ti; // 得到新速度（与顶点有关，不是整个刚体的实际速度，目的是为了获取冲量）

		Matrix4x4 I = Matrix4x4.Rotate(transform.rotation) * I_ref * Matrix4x4.Rotate(transform.rotation).transpose;
		Matrix4x4 K = MatrixSubtraction(MatrixMultiply(Matrix4x4.identity, 1 / mass), Get_Cross_Matrix(Rri) * I.inverse * Get_Cross_Matrix(Rri));
		Vector3 j = K.inverse.MultiplyVector(new_vi - vi); // 获得冲量
        
        // 使用冲量更新刚体的速度和角速度
		v = v + 1 / mass * j;
		w = w + I.inverse.MultiplyVector(Vector3.Cross(Rri, j));
	}

	Matrix4x4 MatrixMultiply(Matrix4x4 m, float n)
	{
		return new Matrix4x4(m.GetColumn(0) * n, m.GetColumn(1) * n, m.GetColumn(2) * n, m.GetColumn(3) * n);
	}

	Matrix4x4 MatrixSubtraction(Matrix4x4 m1, Matrix4x4 m2)
	{
		Vector4 col0 = m1.GetColumn(0) - m2.GetColumn(0);
		Vector4 col1 = m1.GetColumn(1) - m2.GetColumn(1);
		Vector4 col2 = m1.GetColumn(2) - m2.GetColumn(2);
		Vector4 col3 = m1.GetColumn(3) - m2.GetColumn(3);
		return new Matrix4x4(col0, col1, col2, col3);
	}

	// Update is called once per frame
	void Update()
	{
		//Game Control
		if (Input.GetKey("r"))
		{
			transform.position = new Vector3(0, 0.6f, 0);
			restitution = 0.5f;
			launched = false;
		}
		if (Input.GetKey("l"))
		{
			v = new Vector3(5, 2, 0);
			launched = true;
		}

		// Part I: Update velocities
		if (launched == false)
		{
			return;
		}
		v = v + dt * Vector3.down * gravity;
		v = linear_decay * v;
		w = angular_decay * w;

		// Part II: Collision Impulse
		Collision_Impulse(new Vector3(0, 0.01f, 0), new Vector3(0, 1, 0));
		Collision_Impulse(new Vector3(2, 0, 0), new Vector3(-1, 0, 0));

		// Part III: Update position & orientation
		//Update linear status
		Vector3 x = transform.position;
		x = x + v * dt;
		//Update angular status
		Quaternion q = transform.rotation;
		q = QuaternionAddition(q, new Quaternion(w.x * dt / 2, w.y * dt / 2, w.z * dt / 2, 0) * q).normalized;

		// Part IV: Assign to the object
		transform.position = x;
		transform.rotation = q;
	}

	Quaternion QuaternionAddition(Quaternion q1, Quaternion q2)
	{
		return new Quaternion(q1.x + q2.x, q1.y + q2.y, q1.z + q2.z, q1.w + q2.w);
	}
}

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Rigid_Bunny_by_Shape_Matching : MonoBehaviour
{
	public bool launched = false;
	Vector3[] X; // 每个点的位置
	Vector3[] Q; // 每个点的旋转
	Vector3[] V; // 每个点的速度
	Vector3[] Y;
	Matrix4x4 QQt = Matrix4x4.zero;

	Vector3 G = new Vector3(0.0f, -9.8f, 0.0f);
	float linear_decay = 0.999f;
	Vector3 ground = new Vector3(0, 0.01f, 0);
	Vector3 groundNormal = new Vector3(0, 1, 0);
	Vector3 wall = new Vector3(2.01f, 0, 0);
	Vector3 wallNormal = new Vector3(-1, 0, 0);
	float mu_T = 0.5f;  // μ_T may be coefficient of air resistance
	float mu_N = 5.0f; // μ_N may be Coefficient of Restitution

	// Start is called before the first frame update
	void Start()
	{
		Mesh mesh = GetComponent<MeshFilter>().mesh;
		V = new Vector3[mesh.vertices.Length];
		X = mesh.vertices;
		Y = X;
		Q = mesh.vertices;

		//Centerizing Q.
		Vector3 c = Vector3.zero;
		for (int i = 0; i < Q.Length; i++)
			c += Q[i];
		c /= Q.Length;
		for (int i = 0; i < Q.Length; i++)
			Q[i] -= c;

		//Get QQ^t ready.
		for (int i = 0; i < Q.Length; i++)
		{
			QQt[0, 0] += Q[i][0] * Q[i][0];
			QQt[0, 1] += Q[i][0] * Q[i][1];
			QQt[0, 2] += Q[i][0] * Q[i][2];
			QQt[1, 0] += Q[i][1] * Q[i][0];
			QQt[1, 1] += Q[i][1] * Q[i][1];
			QQt[1, 2] += Q[i][1] * Q[i][2];
			QQt[2, 0] += Q[i][2] * Q[i][0];
			QQt[2, 1] += Q[i][2] * Q[i][1];
			QQt[2, 2] += Q[i][2] * Q[i][2];
		}
		QQt[3, 3] = 1;

		for (int i = 0; i < X.Length; i++)
			V[i][0] = 4.0f;

		Update_Mesh(transform.position, Matrix4x4.Rotate(transform.rotation), 0);
		transform.position = Vector3.zero;
		transform.rotation = Quaternion.identity;
	}

	// Polar Decomposition that returns the rotation from F.
	Matrix4x4 Get_Rotation(Matrix4x4 F)
	{
		Matrix4x4 C = Matrix4x4.zero;
		for (int ii = 0; ii < 3; ii++)
			for (int jj = 0; jj < 3; jj++)
				for (int kk = 0; kk < 3; kk++)
					C[ii, jj] += F[kk, ii] * F[kk, jj];

		Matrix4x4 C2 = Matrix4x4.zero;
		for (int ii = 0; ii < 3; ii++)
			for (int jj = 0; jj < 3; jj++)
				for (int kk = 0; kk < 3; kk++)
					C2[ii, jj] += C[ii, kk] * C[jj, kk];

		float det = F[0, 0] * F[1, 1] * F[2, 2] +
						F[0, 1] * F[1, 2] * F[2, 0] +
						F[1, 0] * F[2, 1] * F[0, 2] -
						F[0, 2] * F[1, 1] * F[2, 0] -
						F[0, 1] * F[1, 0] * F[2, 2] -
						F[0, 0] * F[1, 2] * F[2, 1];

		float I_c = C[0, 0] + C[1, 1] + C[2, 2];
		float I_c2 = I_c * I_c;
		float II_c = 0.5f * (I_c2 - C2[0, 0] - C2[1, 1] - C2[2, 2]);
		float III_c = det * det;
		float k = I_c2 - 3 * II_c;

		Matrix4x4 inv_U = Matrix4x4.zero;
		if (k < 1e-10f)
		{
			float inv_lambda = 1 / Mathf.Sqrt(I_c / 3);
			inv_U[0, 0] = inv_lambda;
			inv_U[1, 1] = inv_lambda;
			inv_U[2, 2] = inv_lambda;
		}
		else
		{
			float l = I_c * (I_c * I_c - 4.5f * II_c) + 13.5f * III_c;
			float k_root = Mathf.Sqrt(k);
			float value = l / (k * k_root);
			if (value < -1.0f) value = -1.0f;
			if (value > 1.0f) value = 1.0f;
			float phi = Mathf.Acos(value);
			float lambda2 = (I_c + 2 * k_root * Mathf.Cos(phi / 3)) / 3.0f;
			float lambda = Mathf.Sqrt(lambda2);

			float III_u = Mathf.Sqrt(III_c);
			if (det < 0) III_u = -III_u;
			float I_u = lambda + Mathf.Sqrt(-lambda2 + I_c + 2 * III_u / lambda);
			float II_u = (I_u * I_u - I_c) * 0.5f;


			float inv_rate, factor;
			inv_rate = 1 / (I_u * II_u - III_u);
			factor = I_u * III_u * inv_rate;

			Matrix4x4 U = Matrix4x4.zero;
			U[0, 0] = factor;
			U[1, 1] = factor;
			U[2, 2] = factor;

			factor = (I_u * I_u - II_u) * inv_rate;
			for (int i = 0; i < 3; i++)
				for (int j = 0; j < 3; j++)
					U[i, j] += factor * C[i, j] - inv_rate * C2[i, j];

			inv_rate = 1 / III_u;
			factor = II_u * inv_rate;
			inv_U[0, 0] = factor;
			inv_U[1, 1] = factor;
			inv_U[2, 2] = factor;

			factor = -I_u * inv_rate;
			for (int i = 0; i < 3; i++)
				for (int j = 0; j < 3; j++)
					inv_U[i, j] += factor * U[i, j] + inv_rate * C[i, j];
		}

		Matrix4x4 R = Matrix4x4.zero;
		for (int ii = 0; ii < 3; ii++)
			for (int jj = 0; jj < 3; jj++)
				for (int kk = 0; kk < 3; kk++)
					R[ii, jj] += F[ii, kk] * inv_U[kk, jj];
		R[3, 3] = 1;
		return R;
	}

	// Update the mesh vertices according to translation c and rotation R.
	// It also updates the velocity.
	void Update_Mesh(Vector3 c, Matrix4x4 R, float inv_dt)
	{
		for (int i = 0; i < Q.Length; i++)
		{
			Vector3 x = (Vector3)(R * Q[i]) + c;

			V[i] += (x - X[i]) * inv_dt;
			X[i] = x;
		}
		Mesh mesh = GetComponent<MeshFilter>().mesh;
		mesh.vertices = X;
	}

	void Collision(float inv_dt)
	{
		for (int i = 0; i < Q.Length; i++)
		{
			bool isCol = false;
			isCol = Collision_Impulse(ground, groundNormal, i);

			if (isCol == false)
			{
				Collision_Impulse(wall, wallNormal, i);
			}
		}
	}

	bool Collision_Impulse(Vector3 P, Vector3 N, int i)
	{
		if (Vector3.Dot(X[i] - P, N) < 0)
		{
			if (Vector3.Dot(V[i], N) < 0)
			{
				Vector3 v_ni = Vector3.Dot(V[i], N) * N;
				Vector3 v_ti = V[i] - v_ni;
				float a = Mathf.Max(1 - mu_T * (1 + mu_N) * v_ni.magnitude / v_ti.magnitude, 0);
				v_ni = -mu_N * v_ni;
				v_ti = a * v_ti;
				V[i] = v_ni + v_ti;
				return true;
			}
		}

		return false;
	}

	// Update is called once per frame
	void Update()
	{
		if (Input.GetKey("l"))
		{
			launched = true;
			for (int i = 0; i < V.Length; i++)
			{
				V[i] = new Vector3(5.0f, 2.0f, 0.0f);
			}
		}
		if (Input.GetKey("r"))
		{
			launched = false;
			for (int i = 0; i < V.Length; i++)
			{
				V[i] = new Vector3(4.0f, 0.0f, 0.0f);
			}

			Update_Mesh(new Vector3(0, 0.6f, 0), Matrix4x4.Rotate(transform.rotation), 0);
		}
		float dt = 0.015f;

		if (launched == false)
		{
			return;
		}

		//Step 1: run a simple particle system.
		for (int i = 0; i < V.Length; i++)
		{
			V[i] = V[i] + G * dt;
			V[i] *= linear_decay;
		}

		//Step 2: Perform simple particle collision.
		Collision(1 / dt);

		for (int i = 0; i < V.Length; i++)
		{
			Y[i] = X[i] + V[i] * dt;
		}
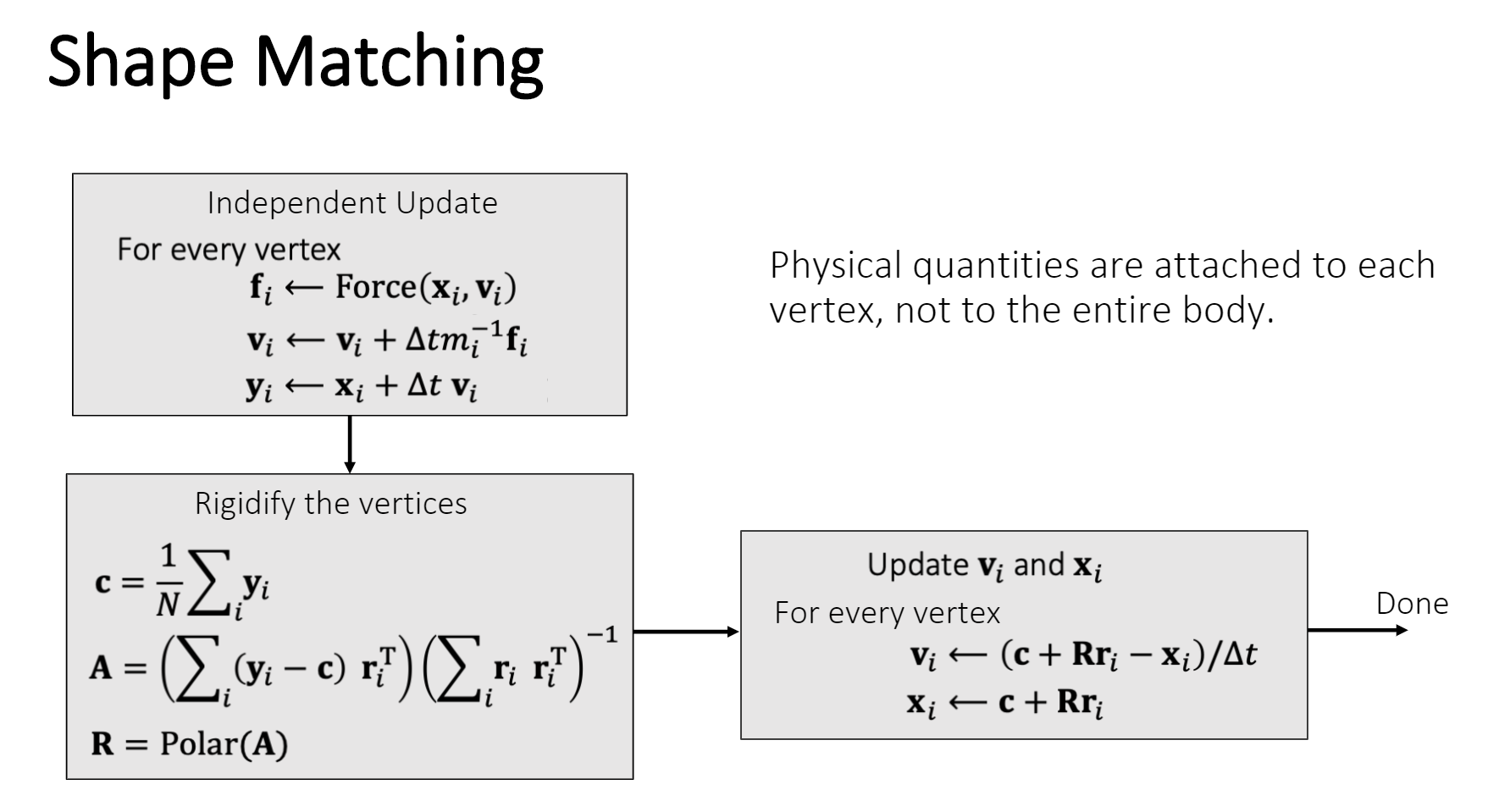
		// Step 3: Use shape matching to get new translation c and 
		// new rotation R. Update the mesh by c and R.
		//Shape Matching (translation)
		Vector3 c = ShapeMatching_translation();
		//Shape Matching (rotation)
		Matrix4x4 R = ShapeMatching_rotation(c);
		Update_Mesh(c, R, 1 / dt);
	}

	Vector3 ShapeMatching_translation()
	{
		Vector3 res = Vector3.zero;
		for (int i = 0; i < Y.Length; i++)
		{
			res = res + Y[i];
		}
		res = res / Y.Length;
		return res;
	}

	Matrix4x4 ShapeMatching_rotation(Vector3 c)
	{
		// calc A
		Matrix4x4 A = Matrix4x4.zero;
		A[3, 3] = 1.0f;
		for (int i = 0; i < V.Length; i++)
		{
			Matrix4x4 o = vector3x1dotvector1x3(Y[i] - c, Q[i]);
			A[0, 0] += o[0, 0];
			A[0, 1] += o[0, 1];
			A[0, 2] += o[0, 2];
			A[1, 0] += o[1, 0];
			A[1, 1] += o[1, 1];
			A[1, 2] += o[1, 2];
			A[2, 0] += o[2, 0];
			A[2, 1] += o[2, 1];
			A[2, 2] += o[2, 2];
		}
		A = A * QQt.inverse;

		//Shape Matching (rotation)
		// calc R
		Matrix4x4 R = Matrix4x4.zero;
		R = Get_Rotation(A);

		return R;
	}


	Matrix4x4 vector3x1dotvector1x3(Vector3 A, Vector3 B)
	{
		Matrix4x4 rlt = Matrix4x4.zero;
		rlt[3, 3] = 1.0f;

		rlt[0, 0] = A[0] * B[0];
		rlt[0, 1] = A[0] * B[1];
		rlt[0, 2] = A[0] * B[2];

		rlt[1, 0] = A[1] * B[0];
		rlt[1, 1] = A[1] * B[1];
		rlt[1, 2] = A[1] * B[2];

		rlt[2, 0] = A[2] * B[0];
		rlt[2, 1] = A[2] * B[1];
		rlt[2, 2] = A[2] * B[2];

		return rlt;
	}
}