游戏编程精粹 游戏编程精粹1

游戏编程精粹1

第一章：通用编程技术

Posted by LudoArt on March 1, 2021

1.0 神奇的数据驱动设计

逻辑部分定义游戏引擎的核心原则和算法，数据部分则提供其内容和行为的具体细节。

1.0.1 基础

创建一个能按需解析文本文件的系统。意义在于——不用修改一行代码，就可以进行各种新尝试。

1.0.2 最低标准

不要用硬编码常量，把常量放进文本文件中。

1.0.3 杜绝硬编码

要假定任何东西都可能（并且很有可能）改变。对游戏进行抽象，把其核心部分抽象处理，要认识到什么才是真正应该建立的，而不只是设计文档中所列举的具有局限性的行为。

1.0.4 将控制流写成脚本

脚本只是一种在代码外定义行为的方法，对于定义游戏中的步骤顺序或需要触发的游戏事件非常有用。

设计脚本语言时，需要考虑一下分支指令，分支有两种方法：一种是把变量保留在脚本语言中，用数学运算符进行比较；另一种是直接调用独立存在于代码中用于比较变量的评价函数。应该使用二者的结合。

1.0.5 什么时候不适合使用脚本

数据驱动的核心思想：将逻辑和数据分开，复杂的逻辑在代码中运行，数据则保留在外面。

1.0.6 避免重复数据

绝对不要复制代码。如果在两个不同的地方需要用相同的行为，这个行为只能存在于一个地方。

1.0.7 开发工具来生成数据

在大型游戏中，文本文件最终会变得不好控制和处理，实际的解决方法是采用一个工具来写这个文本文件。这种工具可以叫做游戏编辑器、关卡编辑器或脚本编辑器。

1.0.8 结论

采用数据驱动方法很容易，但要得到显著的效果却不容易。当所有的东西都采用数据驱动的时候，将拥有无限种发展的可能。

1.1 面向对象的编程与设计技术

1.1.1 代码风格

应尽量保持代码风格的一致性。如匈牙利标注法。但不要在代码规范上做得太过了。

1.1.2 类设计

class Sample
{
    public:
    Sample()	{ Clear(); }
    ~Sample()	{ Destroy(); }
    
    void Clear();
    
    bool Create();
    void Update();
    void Destroy();
};

Clear()函数用于清空所有内部成员变量。

将对象的实际创建点与构造函数分离，就可以动态创建对象一次，但重复调用Create()和Destroy()成员函数来复用同一对象的内存。

Create()函数有两种返回值可以选择：一种是简单的布尔值表示；另一种是使用标准的错误代码类型，通常为符号整型。

Destroy()函数，因为我们既希望有自动清空的便利，又希望有“按需创建和删除”的灵活性，所以我们需要确保Destroy()函数能安全地多次调用，或在没有调用Create()函数的情况下也能安全调用。记住在销毁函数的最后，一定要调用Clear()函数来将所有对象重置回初始状态。

1.1.3 类层次结构设计

扩展类之间的合作主要有两种方法：继承和分层。

  • 继承就是从一个类派生出另一个类；
  • 分层则是指一个对象作为成员包含于另一个对象，也称作组合、容器与嵌套。

有一个简单的原则：如果两个对象之间是“是”的关系，采用公有继承；如果是“有”的关系，则采用分层。

1.1.4 设计模式

  1. Singleton（单件）模式

    当大量的类和/或模块需要访问一个全局对象时，使用Singleton模型。Singleton强迫通过一个类来进行访问，这个类中存储有一个内部静态对象。以下是大致的基本实现形式：

    class Singleton1
{
public:
    Singleton1& Instance()
    {
        static Singleton Obj;
        return Obj;
    }
private:
    Singleton1();
};

    如果要从它派生出新的类，可以改变设计：

    // singleton基类
class SingletonBase()
{
public:
    SingletonBase()
    { cout << "SingletonBase created!" << endl; }
    virtual ~SingletonBase()
    { cout << "SingletonBase destroyed!" << endl; }
    virtual void Access()
    { cout << "SingletonBase accessed!" << endl; }
    static SingletonBase* GetObj()
    { return m_pObj; }
    static void SetObj(SingletonBase* pObj)
    { m_pObj = pObj; }
protected:
    static SingletonBase* m_pObj;
};
   
SingletonBase* SingletonBase::m_pObj;
   
inline SingletonBase* Base()
{
    assert(SingletonBase::GetObj());
    return SingletonBase::GetObj();
}
   
// 创建一个派生的singleton类型
class SingletonDerived : public SingletonBase
{
public:
    SingletonDerived()
    { cout << "SingletonDerived created!" << endl; }
    virtual ~SingletonDerived()
    { cout << "SingletonDerived destroyed!" << endl; }
    virtual void Access()
    { cout << "SingletonDerived accessed!" << endl; }
protected:
};
   
inline SingletonDerived* Derived()
{
    assert(SingletonDerived::GetObj());
    return (SingletonDerived*)SingletonDerived::GetObj();
}
   
// 使用代码
// 复杂的singleton的使用需要做更多工作，而这个更加灵活
// 它还允许对对象创建进行更多的控制，这有时候非常有用
SingletonDerived::SetObj(new SingletonDerived);
   
// 注意这个方法的功能被新类重载了
// 即使通过原有方法访问也是如此
Base()->Access();
Derived()->Access();
   
// 很不幸，singleton上的这个变量要求显示地创建和销毁
delete SingletonDerived::GetObj();

    Scott Bilas所写的《一种自动的singleton工具》文章中提出了对singleton模式的另一种变体，他以一种优雅的方式使用模板和公有继承来自动创建singleton类。

  2. Facade界面模式

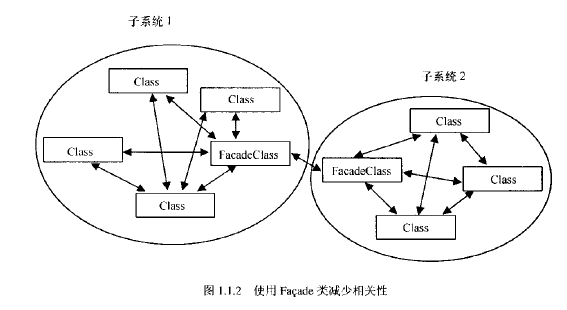
    为了使类之间的相关性（也称作耦合）达到最小，有必要使用Facade或管理器。

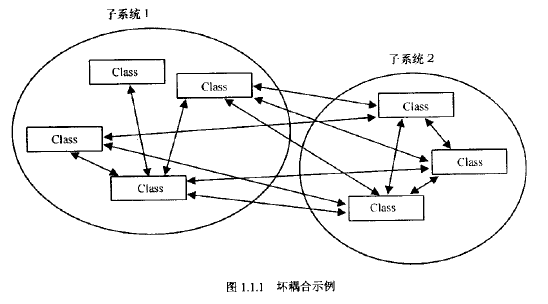
    dfc61686dde49c185d9c394ae81fc41

    实现Facade类的首要原则是：尽量避免子系统内部类对外的暴露。

    681eab08639198f04189f927bd5325e

  3. State（状态）模式

    使用对象的好处是：状态得到了更好的封装，状态可以在它们的基类中逻辑地分享代码，且新的状态可以通过继承轻易地从现有状态中派生出来。 这些好处减少了再离散的状态间进行剪切、粘贴代码所带来的典型问题。

    采用一个中央管理器来处理这些类的过渡，可以避免内部对象之间的关联性，只需要管理器知道所有不同的状态对象就可以了。

  4. Factory（工厂）模式

    Factory模式用于组织对象的创建，它的一种形式定义为一种方法，允许抽象接口类指定何时创建具体的派生实现类。

    把对象分配聚集到一个位置的好处：

    • 因为动态内存分配很昂贵，在一个中央区域分配所有的对象使得分配监控变得更为容易。
    • 通常，全体对象的公共初始化或创建方法应该在一个类层次结构中。如果把对全体对象的分配放到一个中央区域，就使得基于全体对象的操作变得容易了。
    • 工厂具有可扩充性，它允许新的对象从现有工厂中派生出来。通过传递新的类ID，就可以在运行时扩充新的类而不用改变现有的基代码。
    BaseClass* ClassFactory::CreateObject(int id)
{
    BaseClass* pClass = 0;
    switch(id)
    {
        case 1:
            pClass = new Class1;
            break;
        case 2:
            pClass = new Class2;
            break;
        case 3:
            pClass = new Class3;
            break;
        default:
            assert(!"Error!");
    };
       
    pClass->Init(); // 也许需要进行一些一般性的初始化工作
       
    return pClass;
}

    当在一个对象层次结构中的大量对象需要在运行时动态创建的时候，就可以使用工厂模式，这些对象可以包括AI对象、资源或者更抽象的对象。

1.1.5 总结与参考资料

Gamma, et.al., Design Patterns, Addison-Wesley Longman, Inc., 1994.

Meyers, Scott, Effective C++, second edition, Addison-Wesley Longman, Inc., 1996.

Petzold, Charles, Programming Windows 95, Microsoft Press, Inc., 1996.

1.2 使用模板元编程的快速数学方法

注：C++当前标准不支持浮点型作为模板参数使用。

1.2.1 斐波那契数

斐波那契序列形如：0,1,1,2,3,5,8,13,……。该序列的通用方程是： \(Fib(n) = Fib(n-1)+Fib(n-2)\) 递归生成斐波那契数的典型函数如下：

unsigned RecursiveFib(unsigned n)
{
    if(n <= 1)
        return n;
    return RecursiveFib(n - 1) + RecursiveFib(n - 2);
}

其模板化版本如下：

template<unsigned N> struct Fib
{
    enum
    {
        // 递归定义
        Val = Fib<N-1>::Val + Fib<N-2>::Val
    };
};

// 基本情况的模板特殊（结束条件）
template <> struct Fib<0> { enum { Val = 0 }; };
template <> struct Fib<1> { enum { Val = 1 }; };

// 让该模板形如函数
#define FibT(n) Fib<n>::Val

// 通过#define“调用”此模板
std::cout << FibT(4); // Fib<4>::Val

关于此模板化版本需要注意以下几点：

  • 模板函数并不是真正的函数——它是叫做Val的枚举整数，在编译期递归生成。
  • Fib被定义为结构，以简化标记。在默认情况下结构数据是公用的。
  • 模板参数N用于指定函数的输入。
  • 要中止递归，需要正确地处理结束条件。在模板中处理基本情况的方法是使用模板特化。

由于所有的输入在编译期都确定了，所以编译程序可以将FibT(N)换算成常量。即std::cout << FibT(4);等价于std::cout << 3;。

核心思想：用编译时间换取运行时间。

1.2.2 阶乘

标准C++版本：

unsigned RecursiveFact(unsigned n)
{
    return ((n <= 1) ? 1 : (n * RecursiveFact(n - 1)));
}

模板元编程版本：

// 模板化阶乘
template< unsigned N > struct Fact
{
    enum { Val = N * Fact< N - 1 >::Val };
};

// 基本情况的模板特化
template < > struct Fact< 1 >
{
    enum { Val = 1 };
};

// 让模板形如函数
#define FactT(n) Fact< n >::Val

1.2.3 三角学

生成标准三角函数需要采用级数展开。正弦的展开式如下： \(sin(x)=x-(x^3/3!)+(x^5/5!)-(x^7/7!)+(x^9/9!)-…\) 其中x是弧度，0<=x<2π。为了有效计算，将展开式改写为： \(sin(x)=x*term(0)\) 其中term(n)递归计算如下： \(term(n)=1-x^2/(2n+2)/(2n+3)*term(n+1)\) 上述展开式的标准代码如下：

double Sine(double fRad)
{
    const int iMaxTerms = 10;
    return fRad * SineSeries(fRad, 0, iMaxTerms);
}

double SineSeries(double fRad, int i, int iMaxTerms);
{
    if(i > iMaxTerms)
        return 1.0;
    
    return 1.0 - (fRad * fRad / (2.0 * i + 2.0) / (2.0 * i + 3.0) * SineSeries(fRad, i + 1, iMaxTerms));
}

模板化代码如下：

// sin(R)级数展开
// 对符合标准的编译器，将double R改为double& R
template<double R> struct Sine
{
    enum { MaxTerms = 10 }; // 增加精确性
    static inline double sin()
    {
        return R * Series<R, 0, MaxTerms>::val();
    }
};

template<double R, int I, int MaxTerms>
struct Series
{
    enum
    {
        // Continue为true，知道我们已经计算了M项
        Continue = I + 1 != MaxTerms,
        NxtI = (I + 1) * Continue,
        NxtMaxTerms = MaxTerms * Continue;
    };
    
    // 递归定义，
    static inline double val()
    {
        return 1 - R * R / (2.0 * I + 2.0) / 
            (2.0 * I + 3.0) * Series<R * Continue, NxtI, NxtMaxTerms>::val();
    }
};

// 用于终止循环的特化
template<> struct Series<0.0, 0.0>
{
    static inline double val() { return 1.0; }
};

// 使模板能够以类似函数的方式使用
#define SineT(r) Sine<r>::sin()

1.2.4 实际世界中的编译程序

关注对模板的优化以及模板元编程本身。

1.2.5 重访三角学

对正弦函数的另一种尝试：

// sin(R)级数展开
// 对符合标准的编译器，将double R改为double& R
template<double R> struct Sine
{
    // 一个合适的编译器能够把所有在编译器知道的值缩减为一个常量
    static inline double sin()
    {
        double Rsqr = R * R;
        return R * (1.0 - Rsqr / 2.0 / 3.0
                 * (1.0 - Rsqr / 4.0 / 5.0
                 * (1.0 - Rsqr / 6.0 / 7.0
                 * (1.0 - Rsqr / 8.0 / 9.0
                 * (1.0 - Rsqr / 10.0 / 11.0
                 * (1.0 - Rsqr / 12.0 / 13.0
                 * (1.0 - Rsqr / 14.0 / 15.0
                 * (1.0 - Rsqr / 16.0 / 17.0
                 * (1.0 - Rsqr / 18.0 / 19.0
                 * (1.0 - Rsqr / 20.0 / 21.0
                 )))))))));
    }
};
                    
// 使模板能够以类似函数的方式使用
#define SineT(r) Sine<r>::sin()

1.2.6 模板和标准C++

在C++标准中，“一个非类型模板参数不应被声明为浮点类型”，也就是说，在一个遵循标准的编译器中：

template<double R> struct Sine // 编译器错误

解决方法是使用引用参数：

template<double& R> struct Sine // 正确

1.2.7 矩阵

模板元编程的优势所在是处理矩阵运算。

  1. 单位矩阵

    常规的单位矩阵实现：

    matrix33& matrix33::identity()
{
    for(unsigned c = 0; c < 3; c++)
        for(unsigned r = 0; r < 3; r++)
            col[c][r] = (c == r) ? 1.0 : 0.0;
    return *this;
}

    模板化代码：

    // 模板化的单位矩阵，N是矩阵大小
template<class Mtx, unsigned N> struct IdMtx
{
    static inline void eval(Mtx& mtx)
    {
        IdMtxImpl<Mtx, N, 0, 0, 0>::eval(mtx);
    }
};
   
// 对矩阵每个元素赋值
// 矩阵Mtx，矩阵大小N，当前行R和当前列C
// 当I等于N时终止
template<class Mtx, unsigned N, unsigned C, unsigned R, unsigned I> struct IdMtxImpl
{
    enum
    {
        NxtI = I + 1,			// 计数器
        NxtR = NxtI % N,		// 行（内层循环）
        NxtC = NxtI / N % N		// 列（外层循环）
    };
    static inline void eval(Mtx& mtx)
    {
        mtx[C][R] = (C == R) ? 1.0 : 0.0;
        IdMtxImpl<Mtx, N, NxtC, NxtR, NxtI>::eval(mtx);
    }
};
   
// 为3*3和4*4的矩阵特化
template<> struct IdMtxImpl<matrix33, 3, 0, 0, 3*3>
{
    static inline void eval(matrix33) {}
};
template<> struct IdMtxImpl<matrix44, 4, 0, 0, 4*4>
{
    static inline void eval(matrix44) {}
};
   
// 使模板能够以类似函数的方式使用
#define IdentityMtxT(MtxType, Mtx, N) \
		IdMtx<MtxType, N>::eval(Mtx)

    可以将原有版本替换为：

    matrix33& matrix33::identity()
{
    IdentityMtxT(matrix33, *this, 3);
    return *this;
}

    上述代码将被编译器展开为：

    matrix33& matrix33::identity()
{
    col[0][0] = 1.0;
    col[0][1] = 0.0;
    // ……
    col[2][1] = 0.0;
    col[2][2] = 1.0;
    return *this;
}

  2. 矩阵初始化

    我们可以通过在生成单位矩阵中使用过的相同技术来创建模板化的初始化代码。唯一需要改变的是决定每个矩阵元素值的行：

    mtx[C][R] = (C == R) ? 1.0 : 0.0; // 单位矩阵
   
mtx[C][R] = 0.0; // 零矩阵
   
mtx[C][R] = static_cast<F>(Init); // 初始化矩阵

    这里的类型F是存储在每个元素中值的类型，而Init是缺省为0的数字模板参数。这个通用解决方案允许你简单地初始化矩阵元素为任意常量值。

  3. 矩阵变换

    以对角线为轴对矩阵进行翻转变换：

    matrix33& matrix33::transpose()
{
    for(unsigned c = 0;c < 3;c++)
        for(unsigned r = c + 1;r < 3; r++)
            std::swap(cor[c][r], col[r][c]);
    return *this;
}

    3*3的矩阵实际上只有3次交换，这么做将很大程度上损害性能。

    // 模板化的矩阵变化：N是矩阵大小
template<class Mtx, unsigned N> struct TransMtx
{
    static inline void eval(Mtx& mtx)
    {
        TransMtxImpl<Mtx, N, 0, 1, 0>::eval(mtx);
    }
};
   
template<class Mtx, unsigned N, unsigned C, unsigned R, unsigned I> struct TransMtxImpl
{
    enum
    {
        NxtI = I + 1,
        NxtC = NxtI / N % N,
        NxtR = (NxtI % N) + NxtC + 1
    };
    static inline void eval(Mtx& mtx)
    {
        if(R < N)
            std::swap(mtx[C][R], mtx[R][C]);
        TransMtxImpl<Mtx, N, NxtC, NxtR, NxtI>::eval(mtx);
    }
};
   
// 为3*3和4*4的矩阵特化
template<> struct IdMtxImpl<matrix33, 3, 0, 1, 3*3>
{
    static inline void eval(matrix33) {}
};
template<> struct IdMtxImpl<matrix44, 4, 0, 1, 4*4>
{
    static inline void eval(matrix44) {}
};
   
// 使模板能够以类似函数的方式使用
#define TransMtx(MtxType, Mtx, N) \
		TransMtxImpl<MtxType, N>::eval(Mtx)

    可以将原有版本替换为：

    matrix33& matrix33::transpose()
{
    TransMtxT(matrix33, *this, 3);
    return *this;
}

    上述代码将被编译器展开为：

    matrix33& matrix33::transpose()
{
    std::swap(cor[0][1], col[1][0]);
    std::swap(cor[0][2], col[2][0]);
    std::swap(cor[1][2], col[2][1]);
    return *this;
}

    内嵌的for循环将被优化掉，只留下交换操作，Swap本身也是一个内联函数，因此我们将只剩下9条内存移动指令。

  4. 矩阵乘法

    一个常规的非模板实现类似如下代码：

    matrix33& matrix33::opreator *= (const matrix33& m)
{
    matrix33 t;
    for(unsigned r = 0;r < 3;r++)
    {
        for(unsigned c = 0;c < 3;c++)
        {
            t[c][r] = 0.0;
            for(unsigned k = 0;k < 3;k++)
                t[c][r] += col[k][r] * m[c][k];
        }
    }
    *this = t;
    return *this;
}

    对应的模板化代码：

    // 模板化的矩阵乘法，N是矩阵大小
template<class Mtx, unsigned N> struct MultMtx
{
    static inline void eval(Mtx& r, const Mtx& a, const Mtx& b)
    {
        MultMtxImpl<Mtx, N, 0, 0, 0, 0>::eval(r, a, b);
    }
};
   
template<class Mtx, unsigned N, unsigned C, unsigned R, unsigned K, unsigned I> struct MultMtxImpl
{
    enum
    {
        NxtI = I + 1,				// 计数器
        NxtK = NxtI % N,			// 内存循环
        NxtC = NxtI / N % N,		// 列
        NxtR = NxtI / N / N % N		// 行
    };
    static inline void eval(Mtx& r, const Mtx& a, const Mtx& b)
    {
        r[C][R] += a[K][R] * b[C][K];
        MultMtxImpl<Mtx, N, NxtC, NxtR, NxtK, NxtI>::eval(r, a, b);
    }
};
   
// 为3*3和4*4矩阵特化
template<> struct MultMtxImpl<matrix33, 3, 0, 0, 0, 3*3*3>
{
    static inline void eval(matrix33&, const matrix33&, const matrix33&) {}
};
template<> struct MultMtxImpl<matrix44, 4, 0, 0, 0, 4*4*4>
{
    static inline void eval(matrix44&, const matrix44&, const matrix44&) {}
};
   
// 使模板能够以类似函数的方式使用
#define MultMtxT(MtxType, r, a, b, N)	\
		MultMtx<MtxType, N>::eval(r, a, b)

    矩阵乘法的内层循环变成模板参数K，其扩展为N维矩阵迭代器，矩阵乘法将扩展为N为立方体迭代器。

    将原有版本替换为：

    matrix33& matrix33::operator *= (const matrix33& m)
{
    matrix33 t;
    ZeroMtxT(matrix33, t, 3);
    MultMtxT(matrix33, t, *this, m, 3);
    *this = t;
    return *this;
}

1.2.8 总结

模板是以指令流方式直接生成算法的最有效途径。元编程技术可以被扩展用于用途广泛的函数，包括平方根计算、最大公约数、矩阵求逆或排序。

1.3 一种自动的Singleton工具

1.3.1 定义

Singleton是一种对象，它在一个系统中的任何时候只有一个实例。

在游戏中，Singleton的一些常见例子是纹理贴图、文件或用户界面的管理程序。它们每一个都是一个子系统，通常假定从游戏开始时可用，一直持续到游戏关闭。

有一些此类子系统可以通过全局函数和静态变量来实现，例如内存管理程序的malloc()和free()函数，这种子系统不是Singleton。

1.3.2 优点

  • 首先，由于标号非常重要，Singleton提供了概念上的透明。以Singleton调用类并遵循命名约定（如-Mgr、-Api、Global-等），关系到我们系统该类如何被使用的重要细节。
  • Singleton提供了书写的便利性。

1.3.3 问题

  • Q：为什么不直接使用全局对象呢？
  • A：因为全局对象的创建和销毁次序取决于执行时的情况，然而在可移植的方式中这通常是不可预计的。

1.3.4 传统的解决方法

对Singleton的管理代码通常类似如下：

TextureMgr& GetTextureMgr(void)
{
    static T s_Singleton;
    return (s_Singleton);
}

这种解决方法允许singleton按需实例化——在首次函数调用时。该方法便于使用，但是它把singleton的销毁留给了编译程序，要求在应用程序关闭的时候进行销毁。

1.3.5 较好的方法

我们所需要的无非就是追踪singleton的能力，为此我们所需要的是指向它的一个指针。

class TextureMgr
{
    static TextureMgr* ms_Singleton;
    
public:
    TextureMgr(void) { ms_Singleton = this; /*...*/ }
    ~TextureMgr(void) { ms_Singleton = 0; /*...*/ }
    
    // ...
    TextureMgr& GetSingleton(void) { return (*ms_Singleton); }
}

现在可以在任何时候创建和销毁TextureMgr，并且对该singleton的访问就像调用TextureMgr::GetSingleton()一样简单。

但此解决方法还有一点不方便，那就是相同的代码（用于追踪singleton指针）需要加到每个singleton类中。

1.3.6 更好的方法

一种更通用的解决方法是使用模板来自动定义singleton指针，并完成指针设置、查询和清除的工作。它还可以检查（通过assert()）确保没有将singleton实例化多次。最重要的是，可以免费获得所有这些功能，只需要从以下这个简单的类派生就可以：

#include <cassert>

template <typename T> class Singleton
{
    static T* ms_Singleton;
    
    public:
    Singleton(void)
    {
        assert(!ms_Singleton);
        int offset = (int)(T*)1 - (int)(Singleton<T>*)(T*)1;
        ms_Singleton = (T*)((int)this + offset);
    }
    ~Singleton(void)
    {
        assert(ms_Singleton);
        ms_Singleton = 0;
    }
    
    static T& GetSingleton(void)
    {
        assert(ms_Singleton);
        return (*ms_Singleton);
    }
    
    static T* GetSingletonPtr(void)
    {
        return ms_Singleton;
    }
};

template <typename T> T* Singleton <T>::ms_Singleton = 0;

将任何类转换成singleton，只需要按以下3个简单步骤来做：

  • 从Singleton<MyClass>公开派生你的类MyClass。
  • 确保使用前在系统中创建了MyClass的实例。
  • 在系统的任何地方调用MyClass::GetSingleton()来使用对象。

以下是使用该类的例子：

class TextureMgr : public Singleton <TextureMgr>
{
    public:
    Texture* GetTexture(const char * name);
    // ...
};

#define g_TextureMgr TextureMgr::GetSingleton()

void SomeFunction(void)
{
    Texture* stone1 = TextureMgr::GetSingleton().GetTexture("stone1");
    Texture* wood7 = g_TextureMgr.GetTexture("wood7");
    // ...
}

这个Singleton类的唯一目的是在它的派生类型的任何实例创建和销毁时自动注册和注销它们。

它是如何工作的？

  • 所有重要的工作在Singleton的构造函数中完成，在此它计算出派生实例的相对位置，并将结果存储到singleton指针（ms_Singleton)。
  • 派生类可能不仅仅从Singleton派生，这种情况下MyClass的“this”可能与Singleton的“this”不同。解决方法是假设一个不存在的对象在内存的0x1位置上，将次对象强制转换为两种类型，并得到其偏移量的差值。这个差值可以有效地作为Singleton<MyClass>和它的派生类型MyClass的距离，可用于计算singleton指针。

1.3.7 参考文献

Meyers, Scott, More Effective C++, Addison-Wesley Publishing Co., 1995.

CATALOG
    FEATURED TAGS
    人工智能 深度学习 C++ 面试经验 设计模式 游戏服务器 TensorFlow 笔试经验 C++2.0新特性 C# Unity Game AI Behaviour Tree 游戏开发 Unity优化 GAMES课程
    FRIENDS