一共四道
第一道
这一道100%AC,类似于给定邻接矩阵求极大连通子图的个数。
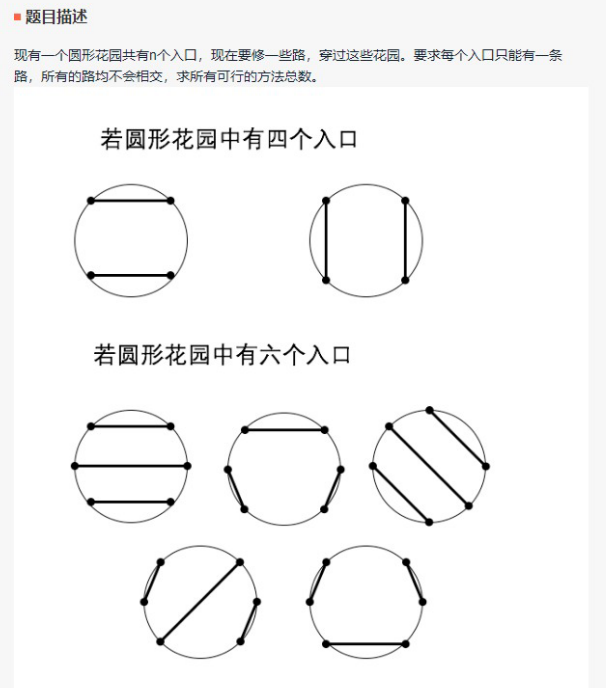
第二道
时间不够没有做完,该题主要还是要找出n个入口m种方法之间的规律,最后的规律可以用一个递归函数来表示,此处贴出代码,因是考试之后才写出来的,所以不知道能不能100%AC(大概应该可能没有问题吧…
#include <iostream>
using namespace std;
int fun(int n) {
if (n == 2)
return 1;
int tmp = n / 2;
int res = 0;
bool flag = false;
if (tmp % 2 != 0) {
flag = true;
tmp++;
}
tmp = tmp / 2;
for (int i = 1; i < tmp; ++i) {
res += fun(n - 2 * i) * 2;
}
if (!flag)
res += fun(n - 2 * tmp) * 2;
else {
int t = fun(n - 2 * tmp);
res += t * t;
}
return res;
}
int main()
{
int n;
cin >> n;
int res;
res = fun(n);
cout << res % 1000000007 << endl;//应题目要求最后做求余操作以简化答案
}
第三道
这道题就是2048游戏的核心呀!分别对上下左右四个方向写了四个函数,不知道是否有更便捷的方法,最后通过率为90%,自己尝试了几个例子也都没有问题,应该是哪里粗心漏了什么,没有例子查不出来…
第四道
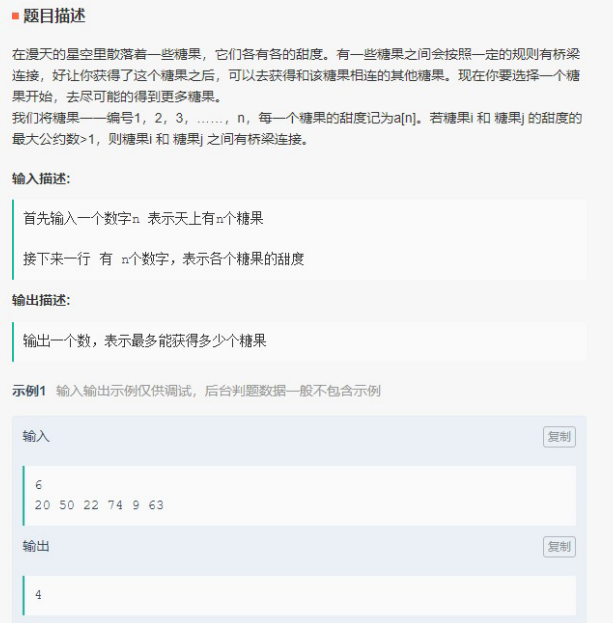
这道题其实和第一题蛮像的,我也基本用了第一题的代码,只不过第一个要求的是极大连通子图的个数,而该题为各个极大连通子图中,节点数最多的那个子图的节点数,求最大公约数的时候,用暴力法AC率为50%,后改为“更相减损法”,AC率70%,再改为“辗转相除法”仍为70%,不知道是否有什么更好的思路,亦或者在求联通子图的时候可以更快些?
总结
下次记得把做题的答案也记录下来,以供之后的修改。